Calibration Curve-fitting

Learning objectives for this section:

• Fit a calibration curve to one run of data using nonlinear regression (4PL):
  • specify non-linear calibration curve functions in R;
    
  • specify a weighting function that reflects change in variance with concentration (RER);
    
  • specify initial values for the parameters of the calibration curve;
    
  • use weighted and unweighted residual plots to evaluate model fit;
    
  • approximate iteratively reweighted least squares (IRLS) regression.
• Calculate the inverse function of the calibration curve and:
  • return predicted concentrations;
    
  • estimate the variance of the predicted concentration.

Unweighted nonlinear regression in R

Unlike linear regression, nonlinear regression models are fit using an iterative algorithm, which requires starting values for each unknown parameter. Based on the plot above and the interpretation of the parameters of the 4PL function, we can visually estimate reasonable starting values. Given the simple structure of the O’Connell data and the strong relationship between concentration and response, starting values do not need to be very accurate.

The mean of the zero-calibrators, 0.1, is a good starting value for parameter \(d\). The upper asymptote, \(a\), looks like it’s going off to a limit of about 1. The \(b\) parameter is harder to imagine, but for an ascending curve, a negative number is needed; -1 will do. From the log(concentration) plot, \(c\), the inflection point, looks like it may be around 8 so on the absolute scale that is 2981.

Let’s enter into R all the components for 4PL curve-fitting:

# ------------ Function: 4PL curve function ---------------------------------
# We actually loaded it ealier with source("../../AMfunctions.R"), 
# but this is what it looks like

M.4pl <- function(x, small.x.asymp, inf.x.asymp, inflec, hill){
    f <- small.x.asymp + ((inf.x.asymp - small.x.asymp)/
                              (1 + (x / inflec)^hill))
    return(f)
}
# ------------- end ---------------------------------------------------------

# Create a vector with the starting values
# (The order of the parameters is important. It determines the list index number in later functions.)
start.ocon <- c(small.x.asymp = 0.1, inf.x.asymp = 1, inflec = 3000, hill = -1)

Let’s fit an unweighted 4PL curve first:

uw.4pl <- nlsLM(od ~ M.4pl(conc, small.x.asymp, inf.x.asymp, inflec, hill), 
                     data = ocon,
                     start = start.ocon)
summary(uw.4pl)

## 
## Formula: od ~ M.4pl(conc, small.x.asymp, inf.x.asymp, inflec, hill)
## 
## Parameters:
##                 Estimate Std. Error t value Pr(>|t|)
## small.x.asymp    0.11767    0.01231   9.561 6.73e-11
## inf.x.asymp      1.04351    0.05440  19.184  < 2e-16
## inflec        3288.68616  650.10993   5.059 1.68e-05
## hill            -0.84729    0.10216  -8.294 1.78e-09
## 
## Residual standard error: 0.04563 on 32 degrees of freedom
## 
## Number of iterations to convergence: 5 
## Achieved convergence tolerance: 0.0000000149

Interpretation of regression output:

• Formula reminds us of the model we specified.

• Parameters lists the final point estimate and standard error for each parameter.

• Residual standard error is the square root of MSE, the unexplained variance.

• Convergence information: Notice that although our starting values were not very accurate, the model converged in only 5 iterations. Sometimes with more complex data structures or with sparse data sets, the algorithm will reach a built-in limit of iterations and we will need to change that limit, choose different starting values or treat some of the parameters as known. We will do this in the “R’s ELISA{gtools}” curve-fitting tutorial.

What we’re looking for in a regression model (in order of importance):

• Convergence.

• Do the parameter estimates look reasonable?

• No model assumption violations: From the residual plots (weighted residuals for weighted models), are the residuals evenly distributed around zero line?

Remember: R^2 and F-tests are not very meaningful with such highly correlated data i.e. known to have a strong relationship between x and y (see the Background).

Using the output for our unweighted nonlinear model, let’s interpret the model using the internal criteria listed above:

• Convergence.

The algorithm converged.

• Do the parameter estimates look reasonable?

The parameter values have the expected sign and are in plausible ranges.

• No model assumption violations…

We can’t answer this with the numerical summary output. Two graphical tools that can help verify regression assumptions are the fitted regression curve and the curve’s standardised residuals. Standardised residuals are the residuals scaled to a normal distribution with standard deviation of 1. The distribution of the residuals can then more easily be judged unacceptably large or small. We wrote a wrapper function, plotDiag to facilitate this:

# plotDiag():
# Enter nlsLM model and overall plot title
plotDiag.nls(uw.4pl, "Unweighted 4PL calibration model for O'Connell's ELISA: uw.4pl")

• No model assumption violations: From the residual plots (weighted residuals for weighted models), are the residuals evenly distributed around zero line?

The fitted curve looks reasonable, but the residual plot illustrates the violation of the homoscedasticity assumption. This indicates that a weighted model is necessary.

Basic weighted curve-fitting

One approach to modeling non-constant variance in a regression model is by assigning a weight to each observation such that the weights are inversely proportional to the variance. As discussed in the previous section, we typically notice an increasing association between the observed response and the response variance. We chose to model this using the power function, \(Var(y|x) = a*E(y|x)^{theta}\), though other functions are possible. Note that \(E(y|x)\) is the predicted value of the response (y) at a given concentration (x). To fit a weighted model within R, we use the weights argument in the nlsLM function. Recall from in the previous section that the best estimate for \(theta\) was 3.

# Weighted 4PL 
# Theta for weighting (from 'Characterising variance')
theta.ocon <- 3
y.curve <- predict(uw.4pl)
w.4pl <- nlsLM(od ~ M.4pl(conc, small.x.asymp, inf.x.asymp, inflec, hill), 
                    data = ocon,
                    start = start.ocon,
                    weights = (1 / y.curve^theta.ocon)
               )
summary(w.4pl)

## 
## Formula: od ~ M.4pl(conc, small.x.asymp, inf.x.asymp, inflec, hill)
## 
## Parameters:
##                  Estimate  Std. Error t value Pr(>|t|)
## small.x.asymp    0.112907    0.002115  53.383  < 2e-16
## inf.x.asymp      1.131557    0.120940   9.356 1.13e-10
## inflec        4501.949633 1569.162177   2.869  0.00723
## hill            -0.738109    0.050578 -14.593 1.07e-15
## 
## Residual standard error: 0.1534 on 32 degrees of freedom
## 
## Number of iterations to convergence: 6 
## Achieved convergence tolerance: 0.0000000149

plotDiag.nls(w.4pl, "Weighted 4PL calibration model for O'Connell's ELISA: w.4pl")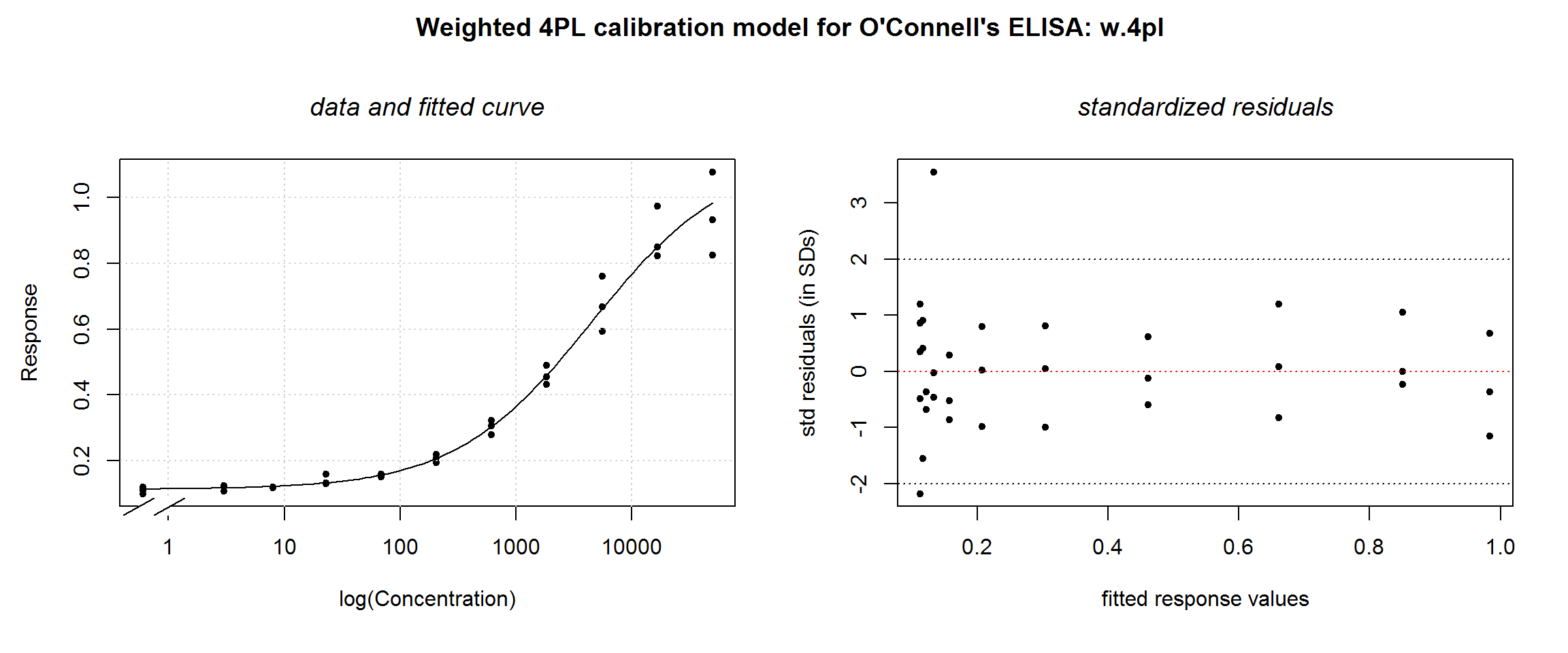

The fitted curve hardly changes, but the residuals look much better. Depending on the outlier criterion you use, one data point (for concentration = 23) may be considered an outlier. We prefer not to exclude borderline questionable points, however—especially when there are so few replicates.

In the original O’Connell tutorial, their modeling algorithm settles on a different value for theta: 2.4; that is, 2 x 1.2 because they use a parameterization in terms of standard deviation rather than variance (1993, 110). Let’s see how a different \(theta\) value affects residuals:

# A different theta, 2.4 (from the O'Connell article)
theta.ocon.lit <- 2.4
w.lit.4pl <- nlsLM(od ~ M.4pl(conc, small.x.asymp, inf.x.asymp, inflec, hill), 
                    data = ocon,
                    start = start.ocon,
                    weights = (1 / y.curve^theta.ocon.lit)
               )
summary(w.lit.4pl)

## 
## Formula: od ~ M.4pl(conc, small.x.asymp, inf.x.asymp, inflec, hill)
## 
## Parameters:
##                  Estimate  Std. Error t value Pr(>|t|)
## small.x.asymp    0.113199    0.002444  46.326  < 2e-16
## inf.x.asymp      1.111586    0.083880  13.252 1.54e-14
## inflec        4189.402732 1117.980807   3.747 0.000708
## hill            -0.750911    0.048126 -15.603  < 2e-16
## 
## Residual standard error: 0.09675 on 32 degrees of freedom
## 
## Number of iterations to convergence: 6 
## Achieved convergence tolerance: 0.0000000149

plotDiag.nls(w.lit.4pl, "Weighted 4PL calibration model for O'Connell's ELISA: w.lit.4pl")

Again, no visible difference in the fitted curve, but the weighted residuals plot changes a little. At this slightly lower value of \(theta\), there seems to still be some increase in the residuals at high response values. A larger data set would be needed to make a definitive choice.

# What are the parts of the model object and summary object
summary(w.4pl)
weights(w.4pl)
mean(weights(w.4pl))
sum(weights(w.4pl))
# Unweighted residuals
resid(w.4pl)
# Unweighted sum of squares - use to compare models
sum(resid(w.4pl)^2)
# Unweighted MSE
sum(resid(w.4pl)^2)/summary(w.4pl)$df[[2]]
# Unweighted RSE
sqrt(sum(resid(w.4pl)^2)/summary(w.4pl)$df[[2]])

# Weighted residuals - use this for plotting
summary(w.4pl)$resid
# Same as 
sqrt(weights(w.4pl))*resid(w.4pl)
# Weighted sum of squares
sum(summary(w.4pl)$resid^2)
# RSE (sigma) - weighted
summary(w.4pl)$sigma